Topological Index Calculator - Sample Examples
Created by Steven Granz - March 2005
Table of Contents:
Adjacency Matrix:
The adjacency matrix of a labeled connected graph G with N vertices is a square
symmetric matrix of order N. This matrix is defined below.
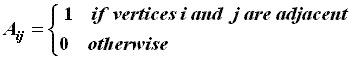
Example: 2,3-dimethylpentane
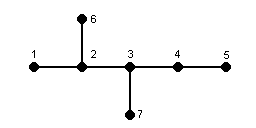
The adjacency matrix of G:
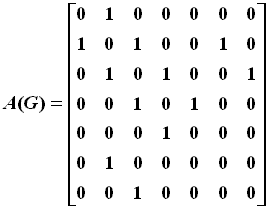
Distance Matrix:
The distance matrix of a labeled connected graph G with N vertices is a square
symmetric matrix of order N. This matrix is defined below.
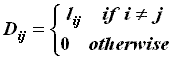
where lij is the length of the shortest path (the distance) between the
vertices i and j in G.
Example: 2,3-dimethylpentane

The distance matrix of G:
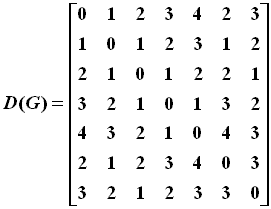
Vertex Degree Vector:
The vertex degree vector of a labeled connected graph G with N vertices
is an (1 x N) vector. This vector is defined below.
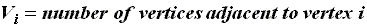
Example: 2,3-dimethylpentane

The vertex degree of G:
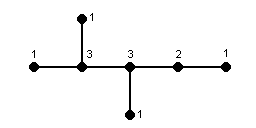
The Vertex Degree Vector of G:
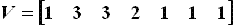
Polarity Index:
The Polarity Index was introduced by Wiener in 1947 as the half the sum of all
the distance matrix entries with a value of 3. This index is defined below.
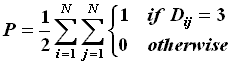
where N is the number of vertices in the molecular graph.
Example: 2,3-dimethylpentane

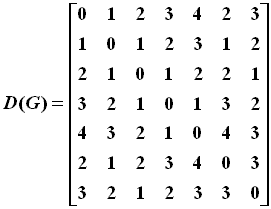
The Polarity Index of G:
P(G) = (12 / 2) = 6
Wiener Index:
The Wiener Index was introduced by Wiener in 1947 as the path number.
This topological index is defined as the half-sum of the elements of the distance matrix.
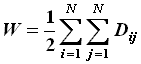
where N is the number of vertices in the molecular graph.
Example: 2,3-dimethylpentane

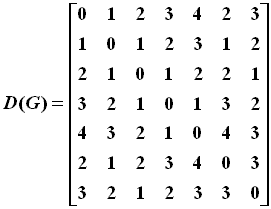
The Wiener Index of G:
W(G) = (15 + 10 + 9 + 12 + 17 + 15 + 14) / 2 = 92 / 2 = 46
Hosoya Index:
The Hosoya Index was introduced by Hosoya in 1971 as the Z index.
This index is defined below.
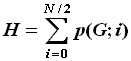
where N is the number of vertices in the molecular graph and
p(G;i) is the number of selections of i mutually non-adjacent edges in G.
By definition, p(G;0) = 1, and p(G;1) is the number of edges in G.
Example: 2,3-dimethylpentane

p(G;0) = 1
p(G;1) = 6
p(G;2) = 8
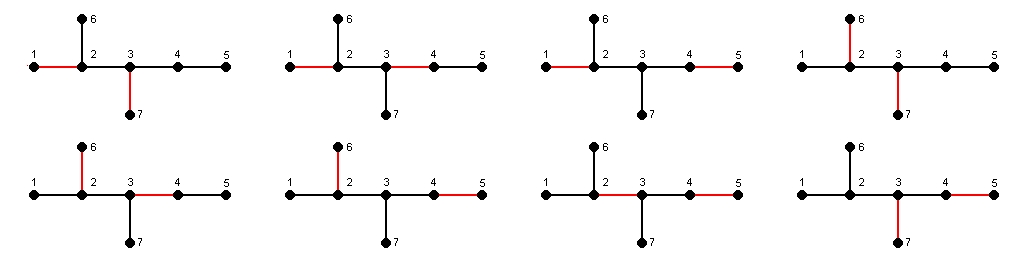
p(G;3) = 2
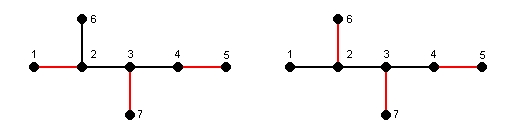
The Hosoya Index of G:
Z(G) = p(G;0) + p(G;1) + p(G;2) + p(G;3) = 1 + 6 + 8 + 2 = 17
Randic Index:
The Randic Index was introduced by Randic in 1975 as the connectivity index.
This index is defined below.
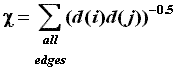
where d(i) and d(j) are the valencies of the vertices i and j that define the edge ij
Example: 2,3-dimethylpentane

The count of the edge-types(the numbers at the vertices represent their valencies)

b12 = 1
b13 = 3
b23 = 1
b33 = 1
The Randic Index of G:
c(G) = 1*0.7071 + 3*0.5774 + 1*.4082 + 1*.3333 = 3.1807
Balaban Index:
The Balaban Index was introduced by Balaban in 1982 as the average-distance sum
connectivity. This index is defined below.
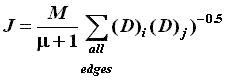
where M is the number of edges in G; m is the cyclomatic number of G;
and (D)i is the distance sum where i = 1,2,...,N.
The cyclomatic number m = m(G) of a polycyclic graph G is equal to the
minimum number of edges that must be removed from G to transform it to
the related acyclic graph. For trees, m = 0; for monocycles, m = 1.
The distance sum (D)i for a vertex i of G represents a sum of all entries
in the corresponding row of the distance matrix.
Example: 2,3-dimethylpentane

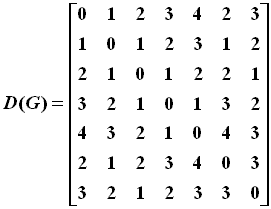
(D)1 = 15
(D)2 = 10
(D)3 = 9
(D)4 = 12
(D)5 = 17
(D)6 = 15
(D)7 = 14
The Balaban Index of G:
J(G) = 6[2*(10*15)-0.5 + (10*9)-0.5 + (9*12)-0.5 + (12*17)-0.5 + (9*14)-0.5] = 3.1442
Harary Index:
The Harary Index was introduced by Plavsic in 1991 in honor of Professor Frank Harary.
This index is defined below.
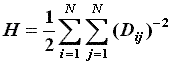
where N is the number of vertices in the molecular graph.
Example: 2,3-dimethylpentane

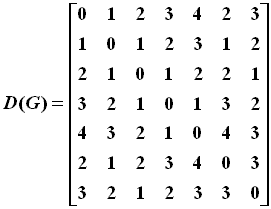

The Harary Index of G:
H(G) = .5(12*1 + 14/4 + 12/9 + 4/16) = 8.5417
Vertex Degree Distance Index:
The Vertex Degree Distance Index was introduced by Cao and Yuan in 2000 as
the degree of the vertices and the distance. This index is defined below.
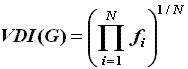
where N is the number of vertices in the molecular graph and
fi is the elements of vector (1xN) VD-2 obtained by V multiply D-2.
VD-2 = [f1,f2,...,fN]
Example: 2,3-dimethylpentane

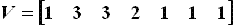

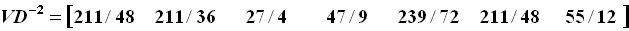
The Vertex Degree Distance Index of G:
VDI(G) = (60739.101)1/7 = 4.8234
Odd-Even Index:
The Odd-Even Index was introduced by Cao and Yuan in 2000 as the sum of the distance
weighted by whether the distance is odd or even. This index is defined below.
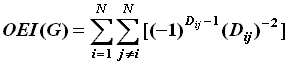
where N is the number of vertices in the molecular graph.
Example: 2,3-dimethylpentane

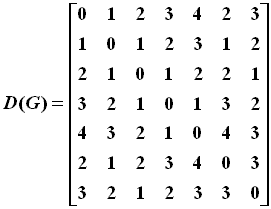

The Odd-Even Index of G:
OEI(G) = 9.5833

