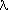 by computing the norm of both sides
by computing the norm of both sides
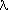 x. If this equation is
true for a particular value of
x. If this equation is
true for a particular value of 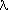 and particular vector x then we say that
and particular vector x then we say that 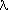 and x
are associated or that they correspond to each other.
and x
are associated or that they correspond to each other.
Given an eigenvector x of A, we can use this equation to find 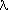 by computing the norm of both sides
by computing the norm of both sides
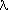 | ||x||
| ||x||
and solving for 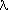 . This gives
. This gives
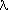 | = ||Ax|| / ||x||
| = ||Ax|| / ||x||
If the vector x is normalized then ||x|| = 1 so things are even simpler:
|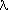 | = ||Ax||.
| = ||Ax||.
Thus, the absolute value (magnitude) of the eigenvalue associated with the eigenvector x is given by ||Ax||.